|
Опять от Гравио - привод генератора из пневмокамеры
| |
| IU | Дата: Пятница, 05.10.2012, 14:18 | Сообщение # 376 |
|
Группа: Пользователи
Сообщений: 372
Статус: Offline
| Quote (RebeLLz) не согласен. для нижней-правой ёмкости в расчётах надо брать площадь левой высокой трубы, и если н/р там площадь 0,1м2, то будет не 16000N, а 1600N.
Нет, неверно. Еще Торричелли экспериментально доказал, что давление в емкости можно поднять до очень большой величины с помощью тонкой трубки наполненной водой. Диаметр трубки не играет никакой роли. Торричелли взял длинную трубку, вставил один конец в бочку, а второй конец поднял на балкон дома. После заполнения тонкой трубки кувшином воды, бочку разорвало гидростатическим давлением. Вот и в нашем случае давление снизу поршня не зависит от диаметра трубки и определяется только высотой столба воды в трубке. На этом принципе работает гидропресс.Добавлено (05.10.2012, 14:18)
---------------------------------------------
Quote (Viknik) Вы наверное не учли в своих расчетах то, что сила, вращающая колесо и сила сопротивления сдавливаемого кармана приложены к колесу в разных точках. У них разное плечо относительно точки опоры "рычага".
Разумеется, у силы, вращающей колесо, плечо больше (чуть меньше радиуса колеса). Точкой опоры "рычага" считаю точку опоры колеса на землю (или на ленту).
Вы могли бы отметить эти рычаги на рисунке МикроГЭС ?
|
| |
| |
| Travler | Дата: Пятница, 05.10.2012, 15:10 | Сообщение # 377 |
|
Группа: Практики
Сообщений: 31
Статус: Offline
| Quote (RebeLLz) Сила F2, с которой жидкость давит на дно сосуда и на поршень, является весом жидкости.
А разве в верхнем сосуде где F2, ГСД высчитывается?! Я считаю нет! Там же просто вес и для этого надо глубину сосуда ещё знать чтобы его вес и этим самым силу весового давления высчитать. Я как понимаю здесь надо весовое давление с ГСД сравнивать а не ГСД с ГСД!
|
| |
| |
| OteЦ | Дата: Пятница, 05.10.2012, 15:16 | Сообщение # 378 |

Группа: Практики
Сообщений: 1156
Статус: Offline
| Quote (Travler) Quote (RebeLLz)Сила F2, с которой жидкость давит на дно сосуда и на поршень, является весом жидкости. А разве в верхнем сосуде где F2, ГСД высчитывается?! Я считаю нет! Там же просто вес и для этого надо глубину сосуда ещё знать чтобы его вес и этим самым силу весового давления высчитать. Я как понимаю здесь надо весовое давление с ГСД сравнивать а не ГСД с ГСД!
всё же ответьте на вопрос:
Почему Вы до сих пор не сделали модель?
С таким убеждением как у Вас я бы уже давно в реальности наблюдал бы это колесо, будь оно рабочее или нет.
Экономьте электричество! выключайте Num_Lock!
|
| |
| |
| Travler | Дата: Пятница, 05.10.2012, 15:34 | Сообщение # 379 |
|
Группа: Практики
Сообщений: 31
Статус: Offline
| Quote (OteЦ) всё же ответьте на вопрос:
Почему Вы до сих пор не сделали модель?
С таким убеждением как у Вас я бы уже давно в реальности наблюдал бы это колесо, будь оно рабочее или нет.
Здравствуйте OteЦ,
я уже один раз писал в форуме у Гравио-1 по поводу этой темы... Люди разные, у меня есть свои причины, про которые я открыто в форуме говорить не хочу. Спасибо за понимания.
А Вы делали модель если не секрет?!
Су
|
| |
| |
| OteЦ | Дата: Пятница, 05.10.2012, 15:51 | Сообщение # 380 |

Группа: Практики
Сообщений: 1156
Статус: Offline
| Quote (Travler) я уже один раз писал в форуме у Гравио-1 по поводу этой темы... Люди разные, у меня есть свои причины, про которые я открыто в форуме говорить не хочу. Спасибо за понимания. А Вы делали модель если не секрет?!
открыто в форуме можно не говорить, для этого существует сервис личных сообщений.
модель этого колеса я не делал,. т.к. мне это не нужно.
Экономьте электричество! выключайте Num_Lock!
|
| |
| |
| IU | Дата: Суббота, 06.10.2012, 00:20 | Сообщение # 381 |
|
Группа: Пользователи
Сообщений: 372
Статус: Offline
| Quote (Travler) А разве в верхнем сосуде где F2, ГСД высчитывается?! Я считаю нет! Там же просто вес и для этого надо глубину сосуда ещё знать чтобы его вес и этим самым силу весового давления высчитать. Я как понимаю здесь надо весовое давление с ГСД сравнивать а не ГСД с ГСД!
Travler, почему Вы решили, что сила от правого сосуда рассчитывается по ГСД ?
RebeLLz прямо пишет "Сила F2, с которой жидкость давит на дно сосуда и на поршень, является весом жидкости". И площадь поперечного сечения правого сосуда RebeLLz указывает - 1 кв.м.
И сравнивается у него ГСД снизу поршня и весовое давление сверху поршня.
Вы просто не внимательно прочитали.
И почему-то не предложили своё решение по этой простой задаче.
Вы и по второй задаче (с мячом) не сообщаете своего решения.
А как Вы тогда сможете понять сложное, если не хотите анализировать простое.
Сообщение отредактировал IU - Суббота, 06.10.2012, 00:25 |
| |
| |
| Travler | Дата: Суббота, 06.10.2012, 11:24 | Сообщение # 382 |
|
Группа: Практики
Сообщений: 31
Статус: Offline
| Полный математический расчет я к сожалению перевести не могу. Я могу конечно так же как и все пару формул из википедии или книги вязать и наверно к тому же результату прейти как например RebeLLz высчитал. Но оно не приведет меня к настоящему пониманию. Это не мой подход к теме. Мой личный подход я описал в сообщение # 363. Но мне нравится Ваш подход IU веник по соломинки разбирать.
Я просто замечании заделал что мне например не совсем ясно как можно весовое давление из внутри круговорота системы определять и его с внутренней противоположной силой сравнивать если весовое давление как бы наружное явление в данной анализированной системе колеса?!
Чтобы объяснить что я конкретно имею виду поставим нашу первую соломинку на весы!

Мы получаем 2 видимых круговорота взаимодействия сил!
1.) Круговорот взаимодействия сил внутреннего вида.(ГСД) Он уравновешивает воду в стаканах. И там тоже есть как бы весовое давлении на дно стакана!
2.) Круговорот взаимодействия сил наружного вида.(весовое давление) Он давит по разному на дно чаш!
ГСД уравновешивает через шланг уровни воды в обоих стаканах с разными диаметрами но весовое давление на чашу весов разные.
Если весам разрешит двигаться из той начальной ситуации как на рисунке, то правая чаша перевесит!
Мы этим самым отделили весовое давление от ГСД!
Теперь обратно к задачки первой соломинки. То что RebeLLz высчитал, скажем наверно правильно. Я не против этого. (Мое замечания касалось конкретней того, что мы слова как "весовое давление" по смыслу смешиваем.)
Заметка, что надо увеличить высоту большого баллона справа до 1,6м что бы уравновесить, тоже я думаю правильная. В схеме нового колеса как раз такого промежутка и нету и виста столба воды уже конструктивно задана и не изменяется и здесь мне припоминается заметка Гравио из Азбуки что надо просто напросто УРАВНОВЕШИВАТь, чтобы создать дисбаланс. (Это просто вывод лично для меня!) Я как понимаю, он не опровергает законы физики а употребляет их в полном объёме как он говорит в Азбуки, значит должны выводы решения задачки 1 правильные быть. (Хотя лично для меня кое какие моменты там не совсем ясны, но я этим сам буду пока разбираться..Надо почитать в это направление по больше мне!)
Что касается мячиков, мне там тоже не ясно то что raiart спросил:
Quote уточнение - если до дна, то во-втором варианте больше
если на диаметр мяча, то одинаково
Что касается вопроса от OteЦ, я ему то написал чтобы и другие знали и не гадали...
Quote У меня самого нету мастерской и инструментов и две левые руки. Мне надо человека найти которого я могу по этому поводу попросить что то заделать. В принципе я нашел такого человека но он не хочет что то делать что он конкретно не понимает и.т.д., Потом, модель делать тоже нету толку, так как работать не будет а на реальную, большую станцию 100% знаний техники и денег пока нету. Я уже как 20 лет темой свободной энергии занимаюсь и многое повидал и то что Гравио пишет как бы с одной стороны интересно и его подход к теме СЕ, чисто по науки тоже интересный а с другой стороны все равно как бы что то не хватает до полного понимания вот может быть вместе и разберемся, мой девиз...
Поэтому, я подчеркиваю, мне нравится подход веник по соломинкам разбирать. Мое убеждении не выражает слепую веру с сторону какого то человека а веру в то что надо просто стараться друг друга понимать. Мое сообщение # 363! Я просто очень сильно стараюсь иногда 
Сообщение отредактировал Travler - Суббота, 06.10.2012, 11:30 |
| |
| |
| IU | Дата: Суббота, 06.10.2012, 13:14 | Сообщение # 383 |
|
Группа: Пользователи
Сообщений: 372
Статус: Offline
| Quote (Travler) ГСД уравновешивает через шланг уровни воды в обоих стаканах с разными диаметрами но весовое давление на чашу весов разные.
Если весам разрешит двигаться из той начальной ситуации как на рисунке, то правая чаша перевесит!
Мы этим самым отделили весовое давление от ГСД!
Согласен, что в начальный момент было равновесие ГСД. Но не было равновесия весового давления - вес правого стакана намного больше.
Правый стакан перевешивает левый в любом случае, даже если их не соединять трубочкой.
Так что, в этом примере нет никакого интересного момента для идеи свободной энергии.
Гравио много раз говорил, что, утапливая мяч в бочке, налитой до краев, мы производим меньше работы, чем утапливая тот же мяч в бочке налитой до половины.
Утопление - это когда весь мяч скрывается под уровнем воды.
Довод Гравио состоит в том, что в бочке, налитой до краев, вода будет вытекать наружу при утоплении мяча, то есть уровень воды не поднимается. А в бочке с половиной воды уровень воды в бочке при утоплении мяча будет подниматься. Вот, мол, отсюда и дополнительная работа по подъёму воды.
На словах - складно, а что же в натуре.
Смотрим картинку.
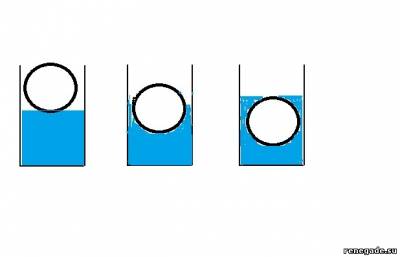
В первой позиции мяч только касается уровня воды. Это точка отсчета. Здесь сила Архимеда равна нулю.
Вторая позиция - мяч погружен в воду на половину диаметра. Уровень воды в бочке при этом поднялся. Сила Архимеда возросла и стала равна весу воды с объёмом в половину мяча.
Третья позиция - мяч полностью под водой. Уровень воды в бочке еще подрос, а сила Архимеда стала равна весу воды с объёмом всего шара F=V*Y. V - объем мяча, Y- удельный вес воды.
Работа по утоплению мяча равна силе, умноженной на путь A=F*L. Здесь L - расстояние на которое опустился мяч. Сила утопления равна по величине и противоположна по направлению силе Архимеда.
Для упрощения можно считать, что сила растет линейно и в среднем равна половине от максимальной силы в конце утопления.
Совершенно очевидно, что в данном варианте утопления путь L меньше диаметра мяча,
При втором варианте утопления, когда бочка полна водой, путь L будет точно равен диаметру мяча.
А сила утопления будет такой же, как в первом варианте.
Стало быть, во втором варианте работы будет затрачено больше, чем в первом.
Это в точности наоборот - по отношению к словам Гравио.
Сообщение отредактировал IU - Суббота, 06.10.2012, 13:16 |
| |
| |
| Viknik | Дата: Суббота, 06.10.2012, 15:34 | Сообщение # 384 |
|
Группа: Пользователи
Сообщений: 375
Статус: Offline
| Quote (IU) При втором варианте утопления, когда бочка полна водой, путь L будет точно равен диаметру мяча.
А сила утопления будет такой же, как в первом варианте.
Стало быть, во втором варианте работы будет затрачено больше, чем в первом.
Это в точности наоборот - по отношению к словам Гравио.
IU, А ведь в первом варианте кроме утопления мяча совершается еще одна работа - по поднятию уровня воды в бочке. Вы про неё забыли? Или считаете, что её учитывать не надо, потому что эта работа уже учтена повышенным сопротивлением мяча при утоплении?Добавлено (06.10.2012, 15:34)
---------------------------------------------
Quote (IU) Работа по утоплению мяча равна силе, умноженной на путь A=F*L. Здесь L - расстояние на которое опустился мяч. Сила утопления равна по величине и противоположна по направлению силе Архимеда.
Если сила утопления мяча равна силе Архимеда, то мяч никуда не потонет. Силы уравновешены. Наверное надо приложить к мячу силу побольше, чтобы он утонул. Мяч будет перемещаться под действием разности сил. Может быть правильнее считать работу этой результирующей силы? Как Вы думаете?
Сообщение отредактировал Viknik - Суббота, 06.10.2012, 14:37 |
| |
| |
| Travler | Дата: Суббота, 06.10.2012, 16:05 | Сообщение # 385 |
|
Группа: Практики
Сообщений: 31
Статус: Offline
| > Так что, в этом примере нет никакого интересного момента для идеи свободной энергии.
Моя мысль с весами еще до конца не развита. Представим теперь такую картину. Правая сторона перевесила, наклонилась, ну скажем на 30° и "пропала" а не месте где она до этого была на первоначальной позиции, заново "появился" новый стакан.
Круговорот взаимодействия сил который мы называем ГСД уравновесит заново воду и наполнит новый стакан. А весовое давление стакана на чашу опусти чашу опять на 30° и.т.д., по кругу.
(Этот пример аллегоричный. Его надо на колесо новой схемы переносить и на старые схемы тоже!)
Поэтому я думаю, всё что RebeLLz высчитал, оно правильное, так как оно часть веника, но только из сумы всех частей получаем нам нужный результат. Но анализ отдельных частей ТОЖЕ нужен. Безусловно!
Нам дали 1000 деталей от самолета. Если мы их все правильно соединим, то самолет полетит. В другом случае не полетит! Каждая деталь сама по себе правильная, расчёты от RebeLLz и IU и.т.д., Ну всё это надо правильно соединить. В чем и вызов.
Пример с мечом!
Ссылка: https://sites.google.com/site....roj-sag
*******
Quote "Для человека далекого от науки,надо просто провести опыт,убедительно доказывающий разницу между работой проталкивания и работой - против сил тяготения.
Достаточно попробовать утопить футбольный мяч в бочке с водою через динамометр.
Мяч,упорно станет сопротивляться но Вы все же погрузите его в воду,- затратив при этом некоторое усилие.
Но если Вы будете погружать тот же мяч в специальную бочку - высота стенок которой уменьшается по мере погружения мяча в воду(вода сливается а не поднимается) то Ваших усилий для погружения мяча под воду потребуется - меньше.
Меньше - ровно в половину - ибо гидростатическое давление на боковую стенку это всегда :высота стенки деленная на два.
То есть, если позволить воде сливаться(течь) а не подниматься то мяч будет погружен в воду как и в первом случае полностью,а работы на "утопленника" потребуется - меньше."
*******
Опять же из девиза стараться правильно понимать то что конкретно имелась ввиду, начинаем рассматривать.
Я думаю, что здесь в примере мяча конкретно другой смысл заложен чем он на первый поверхностный взгляд у нас рождается когда мы слова объяснения воспринимаем.
Суть эксперимента с мячом в том, как я думаю, что в бок воду легче слить или выдавить чем ее вертикально поднять! (Нам не нужен анализ не сил не работы и.т.д., при этом, так как я понимаю, смысловая нагрузка иная была!) Как раз тоже эта "соломинка"(пример с мачом) как часть функции колеса и используется в колесе. Аллегория с мячом нам просто поясняет что в колесе вода не поднимается а просто
а.) уравновешивается, благодаря силе притяжения через ее побочную реакцию ГСД
б.) вода смещается в бок, тоже благодаря силе притяжения
(Мы же не пробуем из "нечего" СЕ получить а из гравитации а она реальная сила?!)
Я уже не однократно упоминал, правда в форуме у Гравио, что его лекции меня больше напоминают коаны. Они имеют особенную функцию информацию передавать! И она не передается через слова те которые использованы были. Слова они в этом случае как забор который ограничивает и указывает направление в которое читателя подталкивают, что бы тот там нашел то понимание что требуется. Это не мистификация, если кто эту мысль подумал. А чистая, философическая наука Герменевтики (искусство толкования, понимания, передачи смысла). У этой науки свои правила как у математики с помощью которых можно определить что правильно истолковано а что в процессе толкования из контекста вырвано.
Так называемый "герменевтический круг" только тогда правильный если мы смысл нового предложения, в данном случаи те объяснения от Гравио, в контексте и на основа старых объяснений рассматриваем.
А с чего всё началось?!
Ссылка: https://sites.google.com/site/gravio/Home/mikroges/azbuka-mikroges
С наблюдения простых наливных колос и удивив в них простые весы было додумано что воду не надо поднимать на много больше уровня перетекания. 1мм достаточно и вода перетекает. (Если этим самым пару тон воды перетекли, они уж свое сделают для выработки энергии!) И у нас есть инерция как свойство материи. Эта инерция нам и даст возможность 1мм преодолеть и река (Гравио) потекла заново и совершила работу на 30°, в зависимости сколько у нас отделов(ковшей, баллонов, ванн и.т.д.,)
ГСД нам всегда поможет всё уравновесить! А инерция нам поможет 1мм дальше пойти и равновесия весов "собьет".
Но остальное наверно технические решения, как колесо притормаживать чтобы из 1мм немного больше стало и вода дальше нам в нужном направление текла а не назад падала вместе с колесом. Нам же надо чтобы колес вращалась а не колебалась и "Активаторы" тоже нужны как аккумулятор силы, для поддержки вращения колеса. У Бесслера например "Активаторы" были 2 маятника... Я не механик, но думаю что вариантов на сегодняшней день намного больше что бы силу "спасти" и в определенный момент обратно внедрить в круговорот колеса.
(Извиняюсь за много орфографических ошибок. Немного торопился, время не было всё проверить!)
Сообщение отредактировал Travler - Суббота, 06.10.2012, 16:08 |
| |
| |
| IU | Дата: Суббота, 06.10.2012, 21:00 | Сообщение # 386 |
|
Группа: Пользователи
Сообщений: 372
Статус: Offline
| Quote (Viknik) IU, А ведь в первом варианте кроме утопления мяча совершается еще одна работа - по поднятию уровня воды в бочке. Вы про неё забыли? Или считаете, что её учитывать не надо, потому что эта работа уже учтена повышенным сопротивлением мяча при утоплении?
В первом варианте работа по поднятию воды в бочке не является дополнительной к работе по утоплению мяча. Поднятие воды – это результат проталкивания мяча в воду. Одна работа равна другой работе со знаком минус.
Во втором варианте вода тоже поднимается. Весь вытесненный мячом объём воды перемещается вверх на половину диаметра мяча, то есть до среза бочки.
Quote (Viknik)
Если сила утопления мяча равна силе Архимеда, то мяч никуда не потонет.
Когда груз с массой m перемещается на высоту Н, то работа по поднятию груза равна mgH.
Если приложить к грузу силу, большую чем его вес, то при поднимании на высоту Н у груза появится еще и скорость, то есть дополнительная энергия.
Также и с утоплением. При очень малой скорости погружения мяча сила проталкивания просто равна силе Архимеда.Добавлено (06.10.2012, 21:00)
---------------------------------------------
Quote (Travler) Представим теперь такую картину. Правая сторона перевесила, наклонилась, ну скажем на 30° и "пропала" а не месте где она до этого была на первоначальной позиции, заново "появился" новый стакан.
Та в этом и есть проблема: как беззатратно доставить стакан воды на прежнюю высоту ?Quote (Travler) Аллегория с мячом нам просто поясняет что в колесе вода не поднимается а просто
а.) уравновешивается, благодаря силе притяжения через ее побочную реакцию ГСД
б.) вода смещается в бок, тоже благодаря силе притяжения
Это иллюзия. При утоплении мяча вода всегда поднимается.
Quote (Travler) С наблюдения простых наливных колос и удивив в них простые весы было додумано что воду не надо поднимать на много больше уровня перетекания. 1мм достаточно и вода перетекает. (Если этим самым пару тон воды перетекли, они уж свое сделают для выработки энергии!)
Ваш пример с обычными водяными колёсами некорректен. Здесь природа позаботилась о поднимании воды. Солнечное тепло испарило воду, которая дождем пролилась в верховье реки.
Где найти хоть один пример о полезной работе "бокового давления воды". Нет таких примеров, чтобы вода поднималась на верхний уровень боковым давлением.
Quote (Travler) У Бесслера например "Активаторы" были 2 маятника...
Какие там маятники Бесслера !
Гравио постоянно твердит, что принцип действия его колес - это физика 7 класса школы.
|
| |
| |
| Viknik | Дата: Воскресенье, 07.10.2012, 16:30 | Сообщение # 387 |
|
Группа: Пользователи
Сообщений: 375
Статус: Offline
| Quote (IU) Второй прутик.
Требуется утопить баскетбольный мяч в бочке с водой.
Первый вариант - бочка наполнена водой наполовину.
Второй вариант - бочка наполнена до краев.
Спрашивается, в каком случае работа по утоплению мяча будет больше ?
Я уверен, что во втором случае работа будет больше.
Ваше мнение ?
Quote (raiart) уточнение - если до дна, то во-втором варианте больше
если на диаметр мяча, то одинаково
Еще одно уточнение. Здесь все зависит от пройденного пути. Возможны различные варианты:
1. Если топить мяч до полного погружения, то во втором варианте затраченная работа будет больше, чем в первом, т.к. перемещение мяча во втором варианте больше.
2. Если силой перемещать мяч вниз на любое, но одинаковое расстояние, хоть до дна, то наоборот - в первом варианте работа будет затрачена больше.
Сообщение отредактировал Viknik - Понедельник, 08.10.2012, 14:03 |
| |
| |
| IU | Дата: Воскресенье, 07.10.2012, 18:38 | Сообщение # 388 |
|
Группа: Пользователи
Сообщений: 372
Статус: Offline
| Quote (Viknik) 1. Если топить мяч до полного погружения, то во втором варианте затраченная работа будет больше, чем в первом, т.к. перемещение мяча во втором варианте больше.
Всё правильно.
Так почему же Гравио утверждает обратное ?
Вероятно, потому, что он не в состоянии подсчитать затраченную работу даже в таком простом примере.
Он думает, раз вода во втором варианте переливается через край бочки, то значит работа на подъём воды не затрачивается.
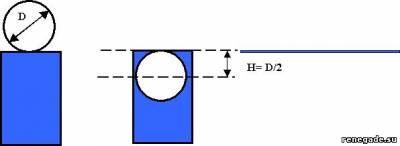
На самом же деле объём воды, равный объёму мяча поднимается вверх на половину диаметра мяча.
И такого рода "проколов" у гениального физика Гравио - на каждом шагу.
Сообщение отредактировал IU - Воскресенье, 07.10.2012, 18:39 |
| |
| |
| Travler | Дата: Понедельник, 08.10.2012, 01:04 | Сообщение # 389 |
|
Группа: Практики
Сообщений: 31
Статус: Offline
| Quote > Та в этом и есть проблема: как беззатратно доставить стакан воды на прежнюю высоту?
Перенося аллегорию со стаканом на колесо, можно себе тот момент как сжатия и раздувания резиновых рюкзаков с водой представить.
Quote >Это иллюзия. При утоплении мяча вода всегда поднимается.
Мой знакомый говорит тоже что работа с мячом одинаковая, что касается погружения меча. (Во втором случает путь для меча длиннее чем в первом варианте а сила меньше чем в первом варианте но работы как бы одинакова в конечном резултате!)
Ссылка: https://sites.google.com/site....roj-sag
"Для человека далекого от науки,надо просто провести опыт,убедительно доказывающий разницу между работой проталкивания и работой - против сил тяготения."
(Работа где вода просто поднимается и работа где вода поднимаясь сразу в сторону увидится!)
Я понимаю это так, что суть аллегории с мячом заключается не в силе и не в работе погружения самого меча в воду а суть в том что воду через край легче в сторону сдвинуть если вода уже до края налита чем воду на верх сначала поднимать. Почему я думая, что именно этот смысл имеется ввиду?! Так как во всех предыдущих размышлениях как раз про эту тему и говорится, что воду в колесе надо
а.) уравновешивать
б.) не нужно воду очень высоко поднимать
а это значит воду мы переливаем просто через край. Конечно вода при этом на пару миллиметров поднимается. Мы совершаем работу но у нас есть инерция движения колеса для одного миллиметра перевеса и уже из гидростатики мы знаем что ГСД от высоты столба воды зависит а это значит если мы немного воды приподнимаем и ее сразу через край в другой ковшик и.т.д переливаем, то мы меньше работы тратим на это действие чем воду просто постоянно на верх поднимать. Я думаю как раз это и хотел Гравио той аллегорией с мячом объяснить. Конечно можно теперь сказать а что 1мм нам даст?! Но а если например в конечном результате 1-а, или 2 или 10 тон воды перельются?! То сколько они смогут энергии на генераторе выработать если эти тоны например на 30° провернутся, то есть опустятся и так определённые пару секунд?!
Вы помните ту первую лекцию с 5-ю кругами?!
Текст задачи:
*************************************
Всего известно 27 типов МикроГЭС от Gravio
Пробуем подобрать Вам один из простейших типов колес.
(учим - как образуется речка Gravio)
Условия задачи:
Колесо имеет пять(сообщающихся)закрытых секций.
Четыре нижних секции полностью заполнены водою.
При этом сохраняется возможность слить часть воды в верхнюю пустую секцию.
Задание - нарисуйте положение колеса при котором слив воды прекратится и колесо остановится.
Успехов.
**************************************

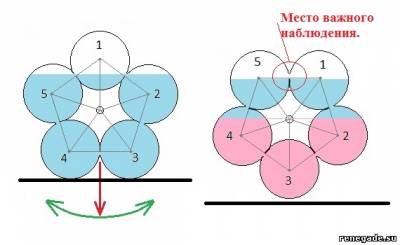
Жмите на рисунок что бы его увеличить!
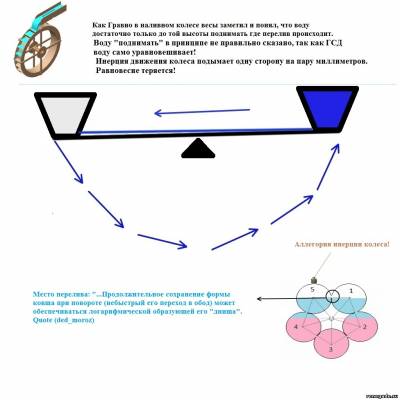
В этом рисунки как раз было заложено понимания того момента как вода чрез край льется в зависимости от диаметра всего колеса и диаметра кругов. Там достаточно 1мм колесо наклонить и вода будет переливается до тех пор пока один круг не станнит пустым! (Что колесо не на оси висит а на полу стоит, Гравио-1 говорил попозже... Получаем рычаг относительно не к оси а к точки прикосновения к земле.)
Добавлено (08.10.2012, 01:04)
---------------------------------------------
Один форумчан(ded_moroz) ответил на задачку так:
Ссылка: https://sites.google.com/site....obsenie
Цитата от ded_moroz:
***************************************
Quote Дата: Среда, Вчера, 01:28 | Сообщение # 1264
В целом представляется так:
1. Давление воды - зеленым цветом рис. 1 - распределено равномерно относительно центра вращения на левую и
правую стороны обода, естественно - в нижней точке обода оно максимально, в правой и левой - минимально. Это - обычное гидростатическое давление.
2. Давление воды в нижней точке левого ковша (широкой части "запятой" - голубым цветом рис.1) составляет примерно половину (по рисунку) глубины воды в ободе, поэтому давление там, соответствующее глубине, составляет примерно половину от гидростатического давления в нижней точке обода "зеленой" воды.
3. Это давление приходится на перегородку, расположенную слева от оси вращения конструкции, следовательно она не может находиться в равновесии и начнет поворачиваться. Давление на перегородку - это весовое давление воды, которое фактически может рассматриваться как вес объекта "наполненный ковш".
4. Молекулы воды в правой "зеленой" части, двигаясь по инерции при вращении конструкции против часовой стрелки, оказываются выше горизонтального уровня и "соскальзывают" к центру вращения, начиная образовывать "почти горизонтальный" поток из правой зеленой половинки справа налево.
5. На ковш, находящийся в правой части в воздухе, молекулы воды давление не оказывают, естественно.
6. В увеличивающуюся в объему пустоту правого уходящего ковша воздух свободно заходит из уменьшающегося хвоста заходящего ковша через пространство обода.
Вывод по вопросу к рис.1: Сила бокового (точнее - находящегося сбоку - слева от вертикальной оси) давления на выпукло - вогнутую стенку появляется при заполнении ковша водой.
Замечание. Если представить на бесконечно малом участке времени, когда еще не сдвинулись молекулы воды, весь
ее объем, как твердое тело - железное, к примеру, то исчезают сомнения - а провернется ли полдиска, если с одной стороны у него висит дополнительный груз, - конечно провернется.
Следствие 1. Чем дальше центр масс ковша с водой от центра вращения - тем больше рычаг, и соответственно развиваемый вращающий момент.
Продолжительное сохранение формы ковша при повороте (небыстрый его переход в обод) может обеспечиваться логарифмической образующей его "днища".
Следствие 2. Если обеспечить заполнение воздухом "уходящего в воздух"ковша из хвоста "заходящего в воду" установкой клапана, то отпадает необходимость в ободе, дистанционирующем ковши, устройство можно преобразовать в цилиндр с S - образной логарифмической перегородкой. В центральной части она должна иметь разрыв для перелива воды из хвоста уходящего ковша во входящий ковш. Уровень воды может быть несколько выше середины для "запирания" воздушного перетока через центральную часть.
Следствие 3. Должны быть сохранены условия обеспечения равного гидростатического давления на правую и левую стороны обода при любых положениях ковшей. Достаточно для этого оставить небольшую щель между барабаном и краями образующей ковшей.
По рис. 2. Все просто. Пусть вода замерзла и колесо так повернули и держат какие-то чудики.
"Зеленой" воды больше, чем "синей", поэтому, если бы не было перетока, после оттаивания, зеленый уровень в правой "запятой" стал бы значительно выше центра, а синий в левой "запятой" - ниже. Но переток через ширину соединяющего "запятые" обода - есть, стало быть часть "зеленой" воды перетечет в "синюю".
Ответ 1. Течение жидкости с одного и того же уровня если строго - это маразм, только если принять что в макроскопическом эксперименте горизонтальность уровня устанавливается почти сразу - да, так с натяжкой можно сказать. Путь - из правого в левый.
Ответ 2. За ПОЛНЫЙ ЦИКЛ, при отсутствии дырок/отверстий/свищей, изменение уровня воды в барабане - не происходит (МАКРО). Но при работе всегда есть МИКРОпревышения уровня на правой стороне.
Поправьте, если где ошибся.
***************************************
Ответ Гравио-1:
***************************************
Quote Quote Quote (ded_moroz)
Ответ 1. Течение жидкости с одного и того же уровня если строго - это маразм, только если принять что в макроскопическом эксперименте горизонтальность уровня устанавливается почти сразу - да, так с натяжкой можно сказать. Путь - из правого в левый.
Ответ 2. За ПОЛНЫЙ ЦИКЛ, при отсутствии дырок/отверстий/свищей, изменение уровня воды в барабане - не происходит (МАКРО). Но при работе всегда есть МИКРОпревышения уровня на правой стороне.
Поправьте, если где ошибся. Поправляю: 1.За "маразм" сынок - большое спасибо... Думаю Gravio этого вполне заслуживает и ...заценит. Что же по сути ответа = неплохо и даже очень неплохо... 2.Лично меня - порадовало Ваше понимание (и это без знаний "Основ гравитационной механики") Ваше: "...Продолжительное сохранение формы ковша при повороте (небыстрый его переход в обод) может обеспечиваться логарифмической образующей его "днища". Это даже и неожиданно ...приятно! Ибо это уже из учебной программы "Курсов". В плане ввода МикроГЭС на бытовой уровень - "каждой кухарке - по плите" - наше ОКБ задачу выполнило. Теперь Вы - можете самостоятельно изготовить МикроГЭС для себя лично и ...соседа. Не забудьте также (хотя бы мелом!) написать мелко-мелко:"водяное колесо Gravio" Ну и разумеется не на украинской мове... Успехов!!! Если человек не хочет делать того,что надо, - пусть он лучше не делает того,- что может... Проверено.
***************************************
Обратите внимание на выражения "...Продолжительное сохранение формы ковша при повороте (небыстрый его переход в обод) может обеспечиваться логарифмической образующей его "днища"
При наклонение чаши то место где вода переливается(край) как бы плоским дном для переливания воды становится.
Оно как раз и описывает тот момент где ковшики наклоняются и вода начинает переливаться. (Зависимость размера колеса от количества масс и их форм, я от других изобретателей гравитационных колос уже слыша, так как это значит очень важно как я думаю.)
Сообщение отредактировал Travler - Понедельник, 08.10.2012, 01:38 |
| |
| |
| Travler | Дата: Понедельник, 08.10.2012, 01:07 | Сообщение # 390 |
|
Группа: Практики
Сообщений: 31
Статус: Offline
| Тот же самый смысл этих двух аспектов
а.) уравновешивать с помощу ГСД
б.) воду высоко не поднимая просто через край лить (а до края воду доносить, нам помогает ГСД)
заложен и в этом рисунки;
Жмите на рисунок что бы его увеличить!

и в этом рисунки;
Жмите на рисунок что бы его увеличить!

и в этом:
Жмите на рисунок что бы его увеличить!
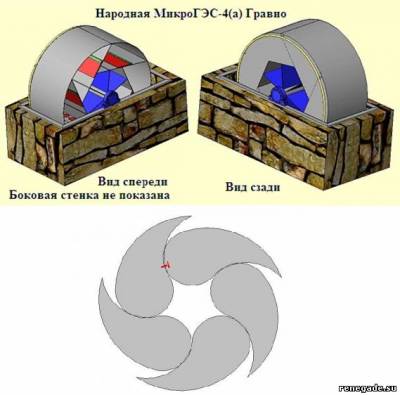
и так же в спиральном колесе;
Жмите на рисунок что бы его увеличить!
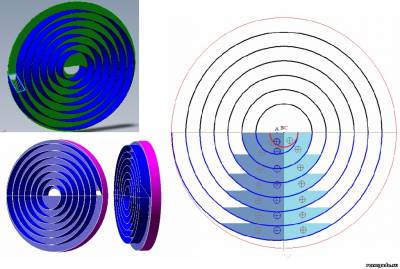
и окончательно в гадюке;
Жмите на рисунок что бы его увеличить!
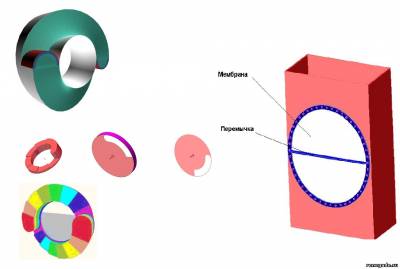
Сообщение отредактировал Travler - Понедельник, 08.10.2012, 01:20 |
| |
| |
|











